Nucleic acid thermodynamics

Nucleic acid thermodynamics is the study of the thermodynamics of nucleic acid molecules, or how temperature affects nucleic acid structure. For multiple copies of DNA molecules, the melting temperature (T_m) is defined as the temperature at which half of the DNA strands are in the double-helical state and half are in the random coil states.^[1] The melting temperature depends on both the length of the molecule, and the specific nucleotide sequence composition of that molecule.

1 Concepts
2 Methods for estimating melting temperatures
- 2.1 Nearest-neighbor method
3 See also
4 References
5 External links

Concepts

Hybridization

Hybridization is the process of establishing a non-covalent, sequence-specific interaction between two or more complementary strands of nucleic acids into a single hybrid, which in the case of two strands is referred to as a duplex. Oligonucleotides, DNA, or RNA will bind to their complement under normal conditions, so two perfectly complementary strands will bind to each other readily. In order to reduce the diversity and obtain the most energetically preferred hybrids, a technique called annealing is used in laboratory practice. However, due to the different molecular geometries of the nucleotides, a single inconsistency between the two strands will make binding between them less energetically favorable. Measuring the effects of base incompatibility by quantifying the rate at which two strands anneal can provide information as to the similarity in base sequence between the two strands being annealed. The hybrids may be dissociated by thermal denaturation, also referred to as melting. Here, the solution of hybrids is heated to break the hydrogen bonds between nucleic bases, after which the two strands separate. In the absence of external negative factors, the processes of hybridization and melting may be repeated in succession indefinitely, which lays the ground for polymerase chain reaction. Most commonly, the pairs of nucleic bases A=T and G≡C are formed, of which the latter is more stable.

Denaturation

DNA denaturation, also called DNA melting, is the process by which double-stranded deoxyribonucleic acid unwinds and separates into single-stranded strands through the breaking of hydrogen bonding between the bases. Both terms are used to refer to the process as it occurs when a mixture is heated, although "denaturation" can also refer to the separation of DNA strands induced by chemicals like urea .

The process of DNA denaturation can be used to analyze some aspects of DNA. Because cytosine / guanine base-pairing is generally stronger than adenosine / thymine base-pairing, the amount of cytosine and guanine in a genome (called the "GC content") can be estimated by measuring the temperature at which the genomic DNA melts.^[2] Higher temperatures are associated with high GC content.

DNA denaturation can also be used to detect sequence differences between two different DNA sequences. DNA is heated and denatured into single-stranded state, and the mixture is cooled to allow strands to rehybridize. Hybrid molecules are formed between similar sequences and any differences between those sequences will result in a disruption of the base-pairing. On a genomic scale, the method has been used by researchers to estimate the genetic distance between two species, a process known as DNA-DNA hybridization.^[3] In the context of a single isolated region of DNA, denaturing gradient gels and temperature gradient gels can be used to detect the presence of small mismatches between two sequences, a process known as temperature gradient gel electrophoresis.^[4]^[5]

Methods of DNA analysis based on melting temperature have the disadvantage of being proxies for studying the underlying sequence; DNA sequencing is generally considered a more accurate method.

The process of DNA melting is also used in molecular biology techniques, notably in the polymerase chain reaction (PCR). Although the temperature of DNA melting is not diagnostic in the technique, methods for estimating T_m are important for determining the appropriate temperatures to use in a protocol. DNA melting temperatures can also be used as a proxy for equalizing the hybridization strengths of a set of molecules, e.g. the oligonucleotide probes of DNA microarrays.

Annealing

Annealing, in genetics, means for DNA or RNA to pair by hydrogen bonds to a complementary sequence, forming a double-stranded polynucleotide. The term is often used to describe the binding of a DNA probe, or the binding of a primer to a DNA strand during a polymerase chain reaction (PCR). The term is also often used to describe the reformation (renaturation) of complementary strands that were separated by heat (thermally denatured).

Proteins such as RAD52 can help DNA anneal.

Methods for estimating melting temperatures

Several formulas are used to calculate T_m values.^[6] ^[7] Some formulas are more accurate in predicting melting temperatures of DNA duplexes. ^[8]

One problem in nucleic acid thermodynamics is to determine the thermodynamic parameters for forming double-stranded nucleic acid AB from single-stranded nucleic acids A and B.

AB ↔ A + B

The equilibrium constant for this reaction is $K=\frac{[A][B]}{[AB]}$ . According to thermodynamics, the relation between free energy, ΔG, and K is ΔG° = -RTln K, where R is the ideal gas law constant, and T is the kelvin temperature of the reaction. This gives, for the nucleic acid system,

$\Delta G^\circ = -RT\ln\frac{[A][B]}{[AB]}$ .

The melting temperature, T_m, occurs when half of the double-stranded nucleic acid has dissociated. If no additional nucleic acids are present, then [A], [B], and [AB] will be equal, and equal to half the initial concentration of double-stranded nucleic acid, [AB]_initial. This gives an expression for the melting point of a nucleic acid duplex of

$T_m = \frac{-\Delta G^\circ}{R\ln\frac{[AB]_{initial}}{2}}$ .

Because ΔG° = ΔH° -TΔS°, T_m is also given by

$T_m = \frac{\Delta H^\circ}{\Delta S^\circ-R\ln\frac{[AB]_{initial}}{2}}$ .

The terms ΔH° and ΔS° are usually given for the association and not the dissociation reaction (see the nearest-neighbor method for example). This formula then turns into ^[1] :

$T_m = \frac{\Delta H^\circ}{\Delta S^\circ%2BR\ln([A]_{total} - [B]_{total}/2)}$ , where [B]_total < [A]_total.

This equation is based on the assumption that only two states are involved in melting: the double stranded state and the random-coil state. However, nucleic acids may melt several intermediate states. To account for such complicated behavior, the methods of statistical mechanics must be used.

Nearest-neighbor method

Some of these parameters can be determined using the nearest-neighbor method. The interaction between bases on different strands depends somewhat on the neighboring bases. Instead of treating a DNA helix as a string of interactions between base pairs, the nearest-neighbor model treats a DNA helix as a string of interactions between 'neighboring' base pairs.^[1] So, for example, the DNA shown below has nearest-neighbor interactions indicated by the arrows.

↓ ↓ ↓ ↓ ↓

5' C-G-T-T-G-A 3'

3' G-C-A-A-C-T 5'

The free energy of forming this DNA from the individual strands, ΔG°, is represented (at 37°C) as

ΔG°₃₇(predicted) = ΔG°₃₇(CG initiation) + ΔG°₃₇(CG/GC) + ΔG°₃₇(GT/CA) + ΔG°₃₇(TT/AA) + ΔG°₃₇(TG/AC) + ΔG°₃₇(GA/CT) + ΔG°₃₇(AT initiation)

The first term represents the free energy of the first base pair, CG, in the absence of a nearest neighbor. The second term includes both the free energy of formation of the second base pair, GC, and stacking interaction between this base pair and the previous base pair. The remaining terms are similarly defined. In general, the free energy of forming a nucleic acid duplex is

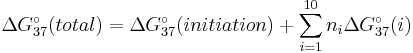$\Delta G_{37}^\circ (total) = \Delta G_{37}^\circ (initiation) %2B \sum_{i=1}^{10} n_i\Delta G_{37}^\circ (i)$ .

Each ΔG° term has enthalpic, ΔH°, and entropic, ΔS°, parameters, so the change in free energy is also given by

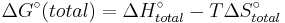$\Delta G^\circ (total) = \Delta H_{total}^\circ - T\Delta S_{total}^\circ$ .

Values of ΔH° and ΔS° have been determined for the ten possible pairs of interactions. These are given in Table 1, along with the value of ΔG° calculated at 37°C. Using these values, the value of ΔG₃₇° for the DNA helix shown above is calculated to be -22.4 kJ/mol. The experimental value is -21.8 kJ/mol.

Table 1. Nearest-neighbor parameters for DNA/DNA duplexes in 1 M NaCl.^[1]
Nearest-neighbor sequence (5'-3'/3'-5')	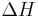$\Delta H$ ° kJ/mol	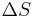$\Delta S$ ° J/(mol·K)	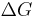$\Delta G$ °₃₇ kJ/mol
AA/TT	-33.1	-92.9	-4.26
AT/TA	-30.1	-85.4	-3.67
TA/AT	-30.1	-89.1	-2.50
CA/GT	-35.6	-95.0	-6.12
GT/CA	-35.1	-93.7	-6.09
CT/GA	-32.6	-87.9	-5.40
GA/CT	-34.3	-92.9	-5.51
CG/GC	-44.4	-113.8	-9.07
GC/CG	-41.0	-102.1	-9.36
GG/CC	-33.5	-83.3	-7.66
Terminal A-T base pair	9.6	17.2	4.31
Terminal G-C base pair	0.4	-11.7	4.05

The parameters associated with the ten groups of neighbors shown in table 1 are determined from melting points of short oligonucleotide duplexes. Curiously, it works out that only eight of the ten groups are independent. A more realistic way of modeling the behavior of nucleic acids would seem to be to have parameters that depend on the neighboring groups on both sides of a nucleotide, giving a table with entries like "TCG/AGC". However, this would involve around 32 groups; the number of experiments needed to get reliable data for so many groups would be considerable. Because the predictions from the nearest neighbor method agree reasonably well with experimental results, the extra effort required to develop a different model may not be justifiable.

References

^ ^a ^b ^c ^d John SantaLucia Jr. (1998). "A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics". Proc. Natl. Acad. Sci. USA 95 (4): 1460–5. doi:10.1073/pnas.95.4.1460. PMC 19045. PMID 9465037. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=19045.
^ M. Mandel and J. Marmur (1968). "Use of Ultravialet Absorbance-Temperature Profile for Determining the Guanine plus Cytosine Content of DNA". Methods in Enzymology 12 (2): 198–206. doi:10.1016/0076-6879(67)12133-2. ISBN 978-0-12-181856-2.
^ C.G. Sibley and J.E. Ahlquist (1984). "The Phylogeny of the Hominoid Primates, as Indicated by DNA-DNA Hybridization". Journal of Molecular Evolution 20 (1): 2–15. doi:10.1007/BF02101980. PMID 6429338.
^ R.M. Myers, T. Maniatis, and L.S. Lerman (1987). "Detection and Localization of Single Base Changes by Denaturing Gradient Gel Electrophoresis". Methods in Enzymology 155: 501–527. doi:10.1016/0076-6879(87)55033-9. PMID 3431470. ISBN 978-0-12-182056-5.
^ T. Po, G. Steger, V. Rosenbaum, J. Kaper, and D. Riesner (1987). "Double-stranded cucumovirus associated RNA 5: experimental analysis of necrogenic and non-necrogenic variants by temperature-gradient gel electrophoresis". Nucleic Acids Research 15 (13): 5069–5083. doi:10.1093/nar/15.13.5069. PMC 305948. PMID 3601667. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=305948.
^ Breslauer, K.J. et al. (1986). "Predicting DNA Duplex Stability from the Base Sequence". Proc. Natl. Acad. Sci. USA. 83 (11): 3746–3750. doi:10.1073/pnas.83.11.3746. PMC 323600. PMID 3459152. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=323600. (pdf)
^ Rychlik, W.; Spencer, W. J.; Rhoads, R. E. (1990). "Optimization of the annealing temperature for DNA amplification in vitro.". Nucleic Acids Res. 18 (21): 6409–6412. doi:10.1093/nar/18.21.6409. PMC 332522. PMID 2243783. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=332522.
^ Owczarzy R., Vallone P.M., Gallo F.J., Paner T.M., Lane M.J. and Benight A.S (1997). "Predicting sequence-dependent melting stability of short duplex DNA oligomers". Biopolymers 44 (3): 217–239. doi:10.1002/(SICI)1097-0282(1997)44:3<217::AID-BIP3>3.0.CO;2-Y. PMID 9591477. (pdf)

External links

Biomolecular structure

Protein structure	Primary · Secondary · Tertiary · Quaternary · Determination · Prediction · Design · Thermodynamics

Nucleic acid structure	Primary · Secondary · Tertiary · Quaternary · Determination · Prediction · Design · Thermodynamics

See also	Protein · Protein domain · Protein engineering · Nucleic acid · DNA · RNA · Nucleic acid double helix